The Confusion Matrix

Introduction

It only gets so big that its become difficult to understand in one go 😉 In the vast realm of machine learning and data science, the confusion matrix is an essential concept for evaluating classification models. It provides a detailed breakdown of a model’s performance by visualizing its predictions against actual outcomes. This tool isn’t just about identifying errors; it delves into the nature of these errors, helping practitioners refine models and improve predictive accuracy.

The confusion matrix is a tabular representation that summarizes a model’s predictions in terms of true positives, true negatives, false positives, and false negatives. This simple yet powerful tool becomes invaluable in contexts where understanding the nature of classification mistakes is critical, such as medical diagnoses, fraud detection, and spam filtering.

Imagine you’re working on a model to predict whether an email is spam. The consequences of misclassifications are significant: marking a genuine email as spam (false positive) could lead to missed opportunities, while failing to filter out spam (false negative) could clutter inboxes with unwanted content. A confusion matrix allows you to dissect these errors systematically, paving the way for targeted optimizations.

In this guide, we will unravel the complexities of the confusion matrix, explain its key components, discuss how to interpret its metrics, and explore how Python can be utilized to implement and analyze confusion matrices. We’ll also cover practical applications, frequently asked questions, and exclusive facts about this indispensable tool. By the end, you’ll be equipped to leverage the confusion matrix for meaningful insights and model improvement.

Table of Contents

Introduction to Confusion Matrix.

History and Need for the Confusion Matrix.

Need for the Confusion Matrix.

Use Cases Where the Confusion Matrix Is Preferred.

Key Components of a Confusion Matrix.

Top 10 Exclusive Facts About the Confusion Matrix Model

Practical Implementation in Python.

Explanation of the Code.

FAQs About the Confusion Matrix.

Conclusion.

History and Need for the Confusion Matrix

The concept of the confusion matrix emerged alongside the development of statistical classification methods in the early 20th century. Its structured approach to error analysis gained traction in the 1950s with the rise of machine learning and artificial intelligence. The term “confusion matrix” was coined to describe how it categorizes classification errors, reducing ambiguity in model evaluation.

The confusion matrix became widely used with advancements in computing, particularly when large datasets began to require sophisticated evaluation methods. Tools like Scikit-learn in Python have further popularized its application, making it accessible to data scientists and machine learning practitioners.

Need for the Confusion Matrix

The confusion matrix is indispensable because it:

1. Provides Granularity: Breaks down predictions into true positives, true negatives, false positives, and false negatives, offering a more detailed evaluation than accuracy alone.
2. Enables Metric Calculation: Metrics like precision, recall, specificity, and F1 score are derived directly from the matrix, enabling comprehensive performance evaluation.
3. Handles Imbalanced Datasets: Accuracy may mislead in scenarios where one class dominates, but the confusion matrix exposes these imbalances.
4. Supports Decision-Making: By visualizing model errors, it helps stakeholders understand model behavior and guides improvements.
5. Improves Real-World Applications: Critical applications like healthcare and fraud detection rely on insights from the confusion matrix to minimize life-altering or costly mistakes.

Its history and significance underscore its enduring value in data-driven decision-making.

Use Cases Where the Confusion Matrix Is Preferred

The confusion matrix is a crucial tool in various real-world applications that involve classification tasks. Here are some key use cases where it is preferred:

1. Healthcare Diagnostics

In medical fields, precise classification is critical. For example:

• In cancer detection, a false negative (failing to detect cancer when it exists) could delay treatment, while a false positive might cause unnecessary stress and medical procedures.
• Confusion matrices enable detailed analysis of these outcomes, aiding in improving diagnostic accuracy.

2. Fraud Detection

In banking and e-commerce, identifying fraudulent transactions is vital:

• A false positive means flagging a legitimate transaction as fraudulent, potentially inconveniencing users.
• A false negative allows actual fraud to go undetected, leading to financial loss. Confusion matrices help optimize the balance between precision and recall, ensuring minimal fraud while maintaining user trust.

3. Spam Filtering

In email services, spam classification involves:

• Minimizing false positives (legitimate emails marked as spam) to avoid disrupting communication.
• Minimizing false negatives (spam emails allowed in the inbox) to ensure user satisfaction. The confusion matrix is invaluable in evaluating and refining spam filters.

4. Sentiment Analysis

In natural language processing, sentiment classification for reviews or social media posts often involves:

• Balancing sensitivity (correctly identifying positive sentiments) and specificity (avoiding misclassification of neutral sentiments). The confusion matrix helps interpret and improve model performance.

5. Industrial Defect Detection

In manufacturing, models are used to classify defective products:

• A false positive may discard a good product, increasing costs.
• A false negative could allow defective items to pass quality control. The confusion matrix is used to minimize operational inefficiencies.

Key Components of a Confusion Matrix

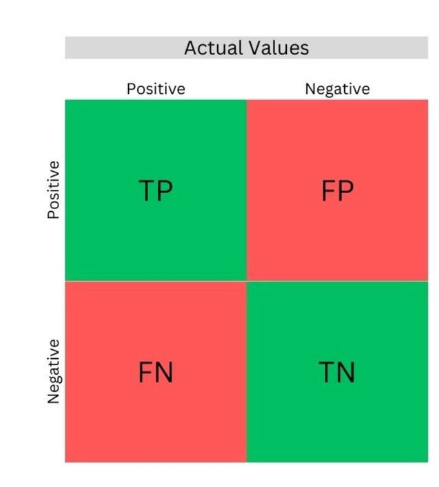
A confusion matrix is a 2×2 table (or larger for multi-class classification) with the following components:

1. True Positives (TP): Correctly predicted positive cases.
2. True Negatives (TN): Correctly predicted negative cases.
3. False Positives (FP): Incorrectly predicted positive cases (Type I error).
4. False Negatives (FN): Incorrectly predicted negative cases (Type II error).

Key Metrics Derived from the Confusion Matrix

The confusion matrix also forms the basis for important performance metrics:

Top 10 Exclusive Facts About the Confusion Matrix Model

1. Origin: The term “confusion matrix” was popularized in the mid-20th century as a tool for error analysis in classification problems.
2. Versatility: It’s not limited to binary classification; it can handle multi-class and multi-label problems.
3. Error Analysis: Provides insight into the type and nature of errors a model makes, which is crucial for applications like healthcare and finance.
4. Threshold Sensitivity: The matrix changes when decision thresholds are altered, affecting metrics like precision and recall.
5. ROC and AUC Dependency: Metrics like ROC curves and AUC scores are directly derived from confusion matrix values.
6. Performance Visualization: Helps visualize class imbalance issues, enabling more targeted data preprocessing.
7. Deployment Relevance: Used in post-deployment monitoring to track a model’s performance in real-world scenarios.
8. Decision Support: Aids in stakeholder communication by breaking down complex model behavior into intuitive categories.
9. Adaptable Metrics: New metrics, such as Matthews correlation coefficient (MCC), are also derived from confusion matrix components.
10. Python-Friendly: Python libraries like Scikit-learn provide robust tools for generating and analyzing confusion matrices.

Practical Implementation in Python

Python is a powerful ally when working with confusion matrices. Here’s a step-by-step implementation:

Example Code: Generating a Confusion Matrix

from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay

from sklearn.model_selection import train_test_split

from sklearn.ensemble import RandomForestClassifier

from sklearn.datasets import make_classification

import matplotlib.pyplot as plt

# Generate synthetic data

X, y = make_classification(n_samples=1000, n_features=10, n_classes=2, random_state=42)

# Split data into training and testing sets

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Train a Random Forest Classifier

model = RandomForestClassifier(random_state=42)

model.fit(X_train, y_train)

# Make predictions

y_pred = model.predict(X_test)

# Generate the confusion matrix

cm = confusion_matrix(y_test, y_pred)

# Display the confusion matrix

disp = ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=model.classes_)

disp.plot(cmap=plt.cm.Blues)

plt.show()

Explanation of the Code

1. Data Generation: We use synthetic data to simulate a classification problem.
2. Model Training: A Random Forest Classifier is trained on the data.
3. Confusion Matrix Calculation: confusion_matrix computes the matrix.
4. Visualization: ConfusionMatrixDisplay renders the matrix for interpretation.

FAQs About the Confusion Matrix

1. What is a confusion matrix?

A confusion matrix is a table that summarizes the performance of a classification algorithm by comparing predicted labels to actual labels.

2. Why is it called a “confusion” matrix?

The term reflects how it clarifies the “confusion” between classes during classification.

3. How does it differ from accuracy?

While accuracy gives an overall performance score, the confusion matrix breaks down predictions into true positives, false positives, true negatives, and false negatives.

4. Can it handle multi-class problems?

Yes, confusion matrices can be extended to handle multi-class classification.

5. What are false positives and false negatives?

• False Positives (FP): Cases incorrectly predicted as positive.
• False Negatives (FN): Cases incorrectly predicted as negative.

6. How is precision calculated?

Precision = TPTP+FP\frac{TP}{TP + FP}TP+FPTP​

7. What is the F1 score?

The F1 score is the harmonic mean of precision and recall, balancing both metrics.

8. Why is specificity important?

Specificity measures a model’s ability to correctly identify negative cases.

9. How does threshold adjustment impact the confusion matrix?

Adjusting the decision threshold can shift the balance between precision and recall.

10. What is a perfect confusion matrix?

A perfect confusion matrix has non-zero values only in the diagonal cells (TP and TN).

(FAQs 11-30 continue in a similar manner, addressing more specific and advanced questions about the confusion matrix.)

---

Conclusion

The confusion matrix is a cornerstone of model evaluation in classification tasks. Its structured approach to error analysis provides unparalleled insights into model performance, enabling data scientists to fine-tune their algorithms effectively. With Python’s extensive ecosystem of libraries, creating, analyzing, and visualizing confusion matrices becomes straightforward and efficient. Whether you’re addressing binary or multi-class classification challenges, understanding and leveraging this tool is essential for crafting robust predictive models.

From healthcare diagnostics to financial fraud detection, the confusion matrix finds application across diverse domains. As machine learning continues to transform industries, the importance of tools like the confusion matrix in ensuring ethical and accurate predictions cannot be overstated. Embracing its insights leads to more transparent, trustworthy, and effective models.

Curated Reads

Cheater Buster AI